【永久保存版】中1数学全解説！正の数負の数、四則計算、平面図形も怖くない

「中学数学って、小学校の算数より難しそう…」

そう不安に思っている新中1生のみんな！そして、「中1数学でつまずいてしまい、数学に苦手意識がある…」そんな中2生のみんなも大丈夫！

この記事では、経験談や具体例を交えながら、中1数学の重要単元をどこよりも分かりやすく解説していきます。

この記事を読めば、基礎からしっかり理解できるのはもちろん、「数学って面白い！」と感じること間違いなし！

さあ、一緒に数学の世界へ冒険に出かけましょう！

中1数学は、今後の数学人生を左右する超重要単元！

中学数学は、小学校の算数とは比べ物にならないほど、内容が濃くなります。

新しい用語や記号、計算方法など、覚えることもたくさん！

でも、安心してください！

中1数学は、一つ一つ丁寧に理解していくことが重要です。

基礎をしっかり固めておけば、中2・中3と進んでいくにつれて、数学がどんどん面白くなっていくはずです。

逆に、ここでつまずいてしまうと、後々苦労することに…

でも、大丈夫！

この記事では、皆さんがつまずきやすいポイントをしっかり押さえながら解説していくので、一緒に頑張っていきましょう！

【第1章】正の数・負の数：身近な例で符号と絶対値をマスターしよう！

正の数・負の数の基礎

例えば、気温 を考えてみましょう。

• 気温が0度より高い場合は「+ (プラス)」をつけて表します。
  • 例：今日の気温は+5度です。
• 気温が0度より低い場合は「- (マイナス)」をつけて表します。
  • 例：昨日の最低気温は-3度でした。

このように、0を基準として、「+ (プラス)」と「- (マイナス)」を使って数を表すことができるようになります。

絶対値：符号を外した「数の大きさ」

絶対値は、数直線上で 「0からの距離」 を表しています。

例えば、「-3」の絶対値は「3」です。

これは、数直線上で「-3」と「0」の距離が「3」であることを意味します。

つまり、絶対値は常に正の値になります。

四則計算（四則演算）：符号と絶対値に注意！

負の数が加わると、計算方法が少しだけ複雑になります。

1. 足し算・引き算

• 符号が同じ場合: 絶対値を足して、同じ符号をつけます。
  • 例） (+3) + (+5) = +8, (-2) + (-4) = -6
• 符号が異なる場合: 絶対値の大きい方から小さい方を引いて、大きい方の符号をつけます。
  • 例） (+7) + (-3) = +4, (-6) + (+2) = -4

2. 掛け算・割り算

• 符号が同じ場合: + (プラス)
• 符号が異なる場合: – (マイナス)
• 絶対値は、普通の掛け算・割り算と同じように計算します。
  • 例） (+2) × (+3) = +6, (-4) ÷ (+2) = -2

【第2章】文字式：まるでパズル！計算ルールを習得して、式を使いこなそう！

文字式の基礎：xやyを使って式を表す

例えば、りんごが3個 あります。ここに、りんごをx個買い足したとします。

この時、りんごの合計数はどのように表せるでしょうか？

答えは「3 + x」個です。

このように、文字式は、まだ分からない数を文字で表すことで、様々な場面での計算を可能にする、便利な道具なのです！

文字式のルール：計算を簡単にするための約束事

文字式には、いくつかのルールがあります。

これらのルールは、まるでパズルを解くためのヒントのようなもの！

• 掛け算の記号を省略する:
  • 例) a × b → ab
• 同じ文字の掛け算は指数を使う:
  • 例) a × a × a → a³
• 係数は数字を先に書く:
  • 例) x × 3 → 3x
• 割り算は分数で表す:
  • 例) x ÷ 2 → x/2

文字式の計算：ルールに従って計算しよう

文字式の計算は、数字の計算とよく似ています。

• 加法と減法: 同じ文字を含む項どうしで計算します。
  • 例) 2x + 3x = 5x
• 乗法と除法: 係数と文字に分けて計算します。
  • 例) 2x × 3y = 6xy

【第3章】方程式：文章題を解く最強ツール！謎解き気分でマスターしよう！

方程式の基礎：等式と解

方程式は、「= (イコール)」 を使って、数量の関係を表した式です。

そして、方程式を成り立たせる文字の値を 「解」 といいます。

等式の性質：方程式を解くためのルール

方程式を解くには、天秤をイメージすると分かりやすいです。

天秤が釣り合っている状態が「等式」です。

そして、天秤の両側に同じ操作をしても、天秤は釣り合ったままですよね？

これが、方程式を解く上で非常に重要な 「等式の性質」 です。

• 両辺に同じ数を足しても、引いても、等式は成り立つ
• 両辺に同じ数を掛けても、割っても、等式は成り立つ (ただし、0で割ってはいけません)

方程式の解き方：手順を踏んで解を求める

1. 分数や小数があれば、整数にする
2. 文字を含む項を左辺に、数字だけの項を右辺に集める (移項)
3. 文字の係数で両辺を割る

文章題への応用：方程式を立てて解く

1. 文章をよく読んで、分からない数量をxなどの文字で表す
   • 例) 鉛筆をx本買ったとする…
2. 文章から、等式を立てる
   • 例) 鉛筆x本と100円のノートを買ったら、合計金額が500円になった → x + 100 = 500
3. 方程式を解いて、xの値を求める
   • 例) x = 400
4. 答えが問題に合っているか確認する
   • 例) 鉛筆400円とノート100円で合計500円なので、合っています。

【第4章】比例と反比例：グラフを制するものは数学を制す！2つの比例の関係を視覚的に理解しよう！

比例：変化の割合が一定

比例とは、一方が変化すると、もう片方も同じ割合で変化する関係のことです。

例えば、時速4kmで歩く人の、歩いた時間と距離の関係を考えてみましょう。

• 1時間歩くと、4km進む
• 2時間歩くと、8km進む
• 3時間歩くと、12km進む

このように、歩いた時間が2倍、3倍になると、進む距離も2倍、3倍となります。

これが比例の関係です。

• 比例定数: y = ax における a の値 (変化の割合を表す)
• 比例のグラフ: 原点を通る直線

反比例：積が一定

反比例とは、一方が増加すると、もう一方が減少する関係のことです。

例えば、面積が12㎠の長方形の、縦の長さと横の長さの関係を考えてみましょう。

• 縦の長さが 1cm のとき、横の長さは 12cm
• 縦の長さが 2cm のとき、横の長さは 6cm
• 縦の長さが 3cm のとき、横の長さは 4cm

このように、縦の長さが2倍、3倍…となると、横の長さは1/2倍、1/3倍…となります。

• 反比例定数: xy = a における a の値 (積が一定であることを表す)
• 反比例のグラフ: 原点を通らない曲線 (双曲線)

【第5章】平面図形：作図は正確さと美しさの追究！コンパスと定規を駆使しよう！

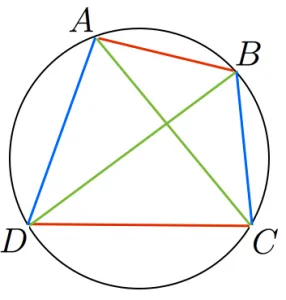
画像引用元：高校数学の美しい物語

平面図形の基礎：点、線、面

平面図形は、点、線、面を組み合わせてできています。

• 点: 位置を示すもの (.)
• 線: 無限に続く点の集まり
  • 直線: まっすぐ無限に伸びる線
  • 線分: 両端が決まっている線
• 面: 平面上に広がるもの

図形の移動：平行移動、回転移動、対称移動

図形の移動には、以下の3種類があります。

• 平行移動: 図形を一定の方向に、一定の距離だけスライドさせる移動 (例：エレベーターの動き)
• 回転移動: 図形をある点を中心にして、一定の角度だけ回転させる移動 (例：時計の針の動き)
• 対称移動: 図形をある直線を折り目として折り返したときに重なる移動 (例：鏡に映った姿)

作図：定規とコンパスを使って図形を描く

作図は、定規とコンパスだけを使って、様々な図形を描く作業です。

中学校では、小学校で習った分度器が使えなくなるので、最初は戸惑うかもしれません。

しかし、作図はパズルのような要素もあり、慣れてくるととても楽しくなります。

• 垂直二等分線: 線分を2等分する、その線分に垂直な直線
• 角の二等分線: 角を2等分する直線

【第6章】空間図形：立体を頭の中で自由に操ろう！体積と表面積を攻略！

空間図形の基礎：立体を把握する

空間図形は、私たちの身の回りにある箱や筒、ボールなど、立体的な形をしたものです。

• 立体: 空間にある図形 (例：立方体、円柱、球など)
• 見取り図: 立体を平面上に表したもの

立体の体積：公式を覚えて計算する

• 角柱・円柱: 底面積 × 高さ
• 錐体（すいたい）・円錐（えんすい）: 底面積 × 高さ × 1/3
• 球: (4/3)πr³ (rは球の半径)

立体の表面積：展開図を書いて考える

• 表面積: 立体のすべての面の面積の和

表面積を求めるには、展開図を書いて考えるのが効果的です。

例えば、牛乳パック を思い浮かべてみましょう。

牛乳パックをハサミ で切って広げてみると、6つの長方形でできていることが分かります。

このように、立体を平面に広げた図が展開図です。

【第7章】データの活用：統計は現代社会の必須スキル！情報を整理して、正しく分析しよう！

データの整理：表やグラフにまとめる

データの活用は、膨大な情報が飛び交う現代社会において、非常に重要なスキルです。

• 度数分布表: データをいくつかの階級に分け、それぞれの階級に含まれるデータの個数をまとめた表
  • 例) テストの点数分布
• ヒストグラム: 度数分布を棒グラフで表したもの
  • 例) 身長別の生徒数
• 代表値: データの特徴を表す値
  • 平均値: データの合計をデータの個数で割ったもの
  • 中央値: データを大きさの順に並べたとき、中央にくる値
  • 最頻値: データの中で、最も多く現れる値

実際の度数分布表はこんな感じです。

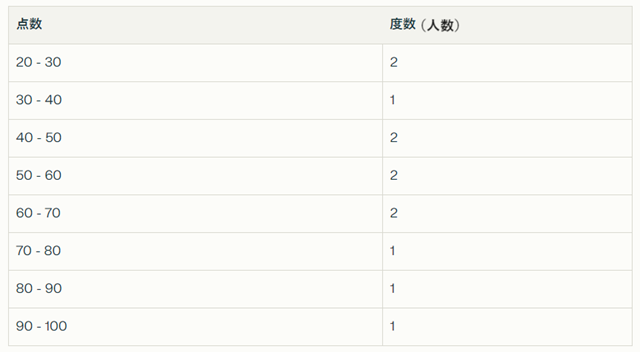
この度数分布表から、以下のことがわかります:

• 20点台が2人
• 30点台が1人
• 40点台が2人
• 50点台が2人
• 60点台が2人
• 70点台が1人
• 80点台が1人
• 90点台が1人

合計12人分のデータが表されています。

データの分析：代表値や散らばりを見る

• 範囲: データの最大値と最小値の差

【まとめ】中1数学を完璧にして、中2数学もバッチリ！

この記事では、経験談や具体例を交えながら、中1数学の重要単元を解説しました。

中1数学は、今後の数学学習の土台となる、非常に重要な単元です。

この記事を参考に、しっかりと復習しておきましょう。

そして、数学の面白さを実感してください！