はじめに
図形と計量では、三角形を基本として様々な図形の角度を、三角比を使って求める問題が出て来ます。
この単元は公式が多く、始め大変かもしれませんが、それらの式といくつかの三角比の値の暗記によってほとんどの問いが解けるようになります。
ここでは図形と計量の基本レベルの理解が簡単になるように、それらの公式のまとめ、活用例を解説します。
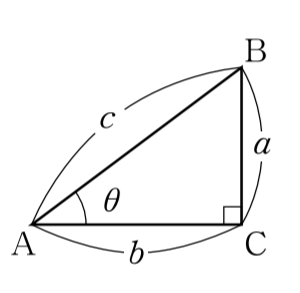
三角比は、∠B=90°の△ABCにおいて、sin∠A=a/b、cos∠A=c/b、tan∠A=a/cのように定義されます。(a、b、cはそれぞれ∠A、∠B、∠Cに相対している辺の長さです。)
このとき、∠Aが30°、45°、60°など三角定規にあるような特別な角度についての値は覚えてしまうことが必要とされています。
三角定規の辺の比をそのまま定義式に対して用いて、
sin∠30°=1/2、cos∠30°=√3/2、tan∠30°=1/√3
sin∠45°=1/√2、cos∠45°=1/√2、tan∠45°=1
sin∠60°=√3/2、cos∠60°=1/2、tan∠60°=√3
ですね。
覚えたこれらの値を足掛かりにして、その他の公式と合わせれば、その他の色々な角度の三角比も求められるようになっています。
また三角比から角度を求めることももちろんあります。
三角比は直角三角形をまずイメージし、そこから辺の比を用いて計算するということから、点Oを中心とする半径rの円周上の任意の点P(x、y)からx軸上に下ろした垂線の足を点Hとし、直角三角形である△OHPを描いて、任意の角度についての三角比を定義することも出来ます。
このとき、∠POH=∠θとすると、sin∠θ=y/r、cos∠θ=x/r、tan∠θ=y/xで、x、yには座標をそのまま当てはめることになっています。つまり三角比の値が正負ともにあり得ることになります。また、θ=0°、90°、180°などの角についても三角比の値が綺麗に分かりますから、それらを覚えることも必要です。分母が0になるときの計算はやらない、つまり解なし扱いとなることには注意しましょう。
また、公式がいくつかあります。
sin(180°-θ)=sinθ、cos(180°-θ)=-cosθ、tan(180°-θ)=-tanθ
sin(90°±θ)=cosθ、cos(90°±θ)=∓sinθ、tan(90°±θ)=∓1/tanθ
です。
これは円周上で実際に180°-θ、90°±θの点Pを作ってみて、そこで△OHPを書き、定義式で比の値を作ってみようとすれば出せます。
だから忘れてしまってもそのようにして思い出すことは出来はします。
180°や90°といった角を基準にとって、そこから±するという発想だけは覚えておきましょう。
sin、cos、tanの間の関係性を表す公式もあります。
sin^2(θ)+cos^2(θ)=1、tanθ=sinθ/cosθ、1+tan^2(θ)=1/cos^2(θ)
です。
これらの式と、あとは正弦定理、余弦定理と呼ばれるものを覚えておけば、図形と計量において角度を求めることに使う式はほとんど網羅出来ているのではないでしょうか。あとは問題の定石暗記の話になってくると思います。それなので、まずはこれらの公式を完全にインプットし問題演習してしまうことをおすすめします。そのあと定石暗記をしていくと効率がよいでしょう。
正弦定理は△ABCについて、その外接円の半径をRとしたとき
a/sin∠A=b/sin∠B=c/sin∠C=2R
余弦定理は、△ABCについて
a^2=b^2+c^2+2bc*cos∠A、b^2=c^2+a^2+2ca*cos∠B、c^2=b^2+a^2+2ba*cos∠C
が成り立つというものです。
代表的問題と解き方です、次の問題演習で感覚をつかんでみてください。
1.問題)0°≦θ≦180°の角θに関して次の問いに答えよ。
(1)sinの値が√3/2になる角度を答えよ。
(2)cosの値が0になる角度を答えよ。
(3)sinの値が0になる角度を答えよ。
(4)cosの値が1になる角度を答えよ。
(5)sinの値が1になる角度を答えよ。
2.問題)辺の長さがa=5、b=4、c=3の△ABCについて、余弦定理を使って∠Aの角度を求めよ。
3.問題)直線l:y=x、直線m:y=(1/√3)x+2のとき、直線l、mが成す角のうち小さい方を求めよ。
1.回答)
(1)
このようなはっきりと鈍角まで扱うと言っている問題は、円周上の任意の点から三角比をとらえる方の定義を使うことが向いていますが、その際任意の値である円の半径を、とりわけr=1として単位円を使って考えてしまうと楽です。0°≦θ≦180°においてsinの値が正の角度は、二つ定まることに気付くことがポイントになります。θ=60°、180°-60°となりますから、答えは60°、120°です。
(2)cos=0になる角度を答えよ。
円周上でx座標が0である点の動径がx軸となす角が求めるものになりますから、90°。
(3)sin=0になる角度を答えよ。
円周上でy座標が0である点の動径がx軸となす角が求めるものになりますから、0°、180°。
(4)cos=1になる角度を答えよ。
円周上でx座標が1である点の動径がx軸となす角が求めるものになりますから、0°。このとき180°についてはcosは-1になるので答えとは違います。
(5)
円周上でy座標が1である点の動径がx軸となす角が求めるものになりますから、90°。
2.回答)
角度を求めるということで、余弦定理を角度に関する式の形と見えるように変形すると、
cos∠A={a^2-(b^2+c^2)}/2bc={25-(16+9)}/2*4*3=0/24=0
従って∠A=90°と求められます。
3.回答)
円周上で任意の角度θについてtanθ=y/xが成り立つということは、一次直線における傾きがその直線とx軸とが成す角のtanに等しくなることもまた表していますが、この設問はそれを使って解く問題です。直線l、mがx軸と成す角をそれぞれθ1、θ2とおくと、tanθ1=1、tanθ2=1/√3よりθ1=45°、θ2=30°です。するとθ2を内角の一つとし、直線lとmで囲まれる三角形に関して外角の公式が適用出来ます。求めたい角度をθとおくと、θ+30°=45°であることからθ=45°-30°=15°。
まとめ
3.の問題はどちらかと言えば、解法を覚えるべきと言われる定石問題に当たるでしょう。
角度の値を突き止めるような問題では他に、三角比が変数として扱われる方程式、不等式を解く三角方程式、三角不等式の問題がよく出て来ます。
これらではsin、cosなどの値をまず変数とし、次にθを変数とする感覚で解きます。
三角比の値を求めて終わることと比べ、θまではっきり求められる場合は少ないですが、問いのそのときの様子をよく見て、解くべきときはそこまで出すのを忘れないようにしましょう。



コメント